
Zadanie Szeregowanie czynności (sze)
Pomóż nam usprawnić bazę zadań!
Job Scheduling
Memory limit: 32 MB
We are given  independent and indivisible jobs numbered from
independent and indivisible jobs numbered from
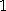 to
to  . They should be executed sequentially in any order.
The later the execution of a job starts the longer it lasts - precisely, the
time of execution of the job
. They should be executed sequentially in any order.
The later the execution of a job starts the longer it lasts - precisely, the
time of execution of the job 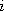 is
is 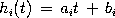 , if we start it in the moment
, if we start it in the moment 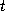 . We assume that
. We assume that 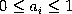 ,
, 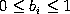 .
.
The goal is to schedule the jobs so that the total execution time is the shortest.
Task
Write a program that:
- reads from the standard input the number of jobs
 not greater
than
not greater
than 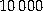 and successively - for each job
and successively - for each job 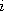 - the
coefficients
- the
coefficients 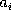 and
and 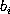 determining the dependence of the
job execution time upon the time it starts,
determining the dependence of the
job execution time upon the time it starts, - finds such a scheduling of the jobs that the cumulative execution time is minimal; then the program writes to the standard output the numbers of the jobs in the order they should be executed.
Input
- In the first line of the standard input there is one positive integer not
greater then
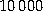 . It is the number of jobs
. It is the number of jobs  .
. - In each of the following
 lines there is a pair of nonnegative
real numbers. The numbers are written in a standard form with a decimal point
and six digits after the point. The numbers are separated by a single space. It
is the pair of coefficients
lines there is a pair of nonnegative
real numbers. The numbers are written in a standard form with a decimal point
and six digits after the point. The numbers are separated by a single space. It
is the pair of coefficients 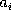 and
and 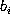 determining the
dependence of the execution time of the corresponding
determining the
dependence of the execution time of the corresponding 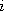 -th job upon
the time it starts.
-th job upon
the time it starts.
Output
One should write in the standard output the scheduling of the jobs, i.e. an
appropriate permutation of numbers 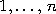 ; one number per
line.
; one number per
line.
Example
For the input data:
5 0.002000 0.003000 0.016000 0.001000 0.100000 0.300000 0.016000 0.005000 0.030000 0.060000
the correct result is:
2 4 1 5 3
Task author: Marcin Jurdzinski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English